Prepositional

What is Logic?

Logic is concerned with all kinds of reasoning, whether they may be legal arguments or mathematical proofs or conclusions in a scientific theory based upon a set  of hypothesis. 

Propositional logic:

It is the simplest form of logic. Here the only statements that are considered are propositions, which contain no variables.  

Because propositions contain no variables, they are either always true or always 

false.

Examples of propositions:

 • 2 + 2 = 4. (Always true)

 • 2 + 2 = 5. (Always false)

Examples of non-propositions:

• x + 2 = 4. (May be true, may not be true; it depends on the value of x.)

• x · 0 = 0. (Always true, but it’s still not a proposition because of the variable.)

• x · 0 = 1. (Always false, but not a proposition because of the variable.)

Sentential Connectives:

To construct rather complicated statements from simpler statements by using certain connecting words 

or expressions.

Atomic or Primary or Primitive:

Declarative sentences which can' be further split into simple statements 

Example: I'm a Professor.

Composite Statements:

New statements can be formed from atomic statements through the use of connectives.

Example: I'm a Professor and Animation Director.

~ In our everyday language we use connectives such as "and", "but", "or", etc., to combine two or more 

statements to form other statements they resulting statements are called Compound or Molecular

Statements.

Statement or Propositions:

It is a statement that is either true or false but not both.

Example:

~ Tirunelveli is a one of district in Tamil Nadu ->True

~ 1 + 1 = 2 -> True

~ 3 - 5 = 7 -> False

Compound Propositions:

They are formed from existing propositions using logical operators.

"T" is denoted by True in a truth table

"F" is denoted by False in a truth table

Truth value:

The truth or falsehood of a proposition

Truth Table:

A table, giving a truth values of a compound statement in terms of its compound parts.

Connectives:

They are used for making compound propositions,

Negation:

The negation of a statement is generally formed by introducing the word "NOT" at a proper place in the 

statement.

~ If "P" denotes a statement, then the negation of "P" is written as " ¬P" and read as "IS NOT P or 

NOT P" and also logic gate in NOT.

~ The truth value of "P" is True / T

~ The truth value of "¬P" is False / F

Example:

Proposition                         : Today is Wednesday

Negation of Proposition    : Today is not Wednesday

Conjunction:

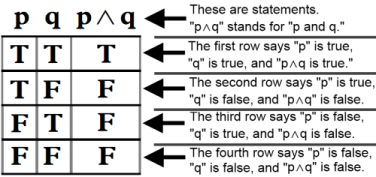
~ The conjunction of two statements P and Q is the statement which is read as "".

~ Whether both P and Q have the truth value T; Otherwise it has the truth value F.

Example:

P: It is raining today.

Q: There are 20 tables in this room.

SOLUTION: It is raining today and there are 20 tables in this room.

Normally, In our everyday language the conjunction "and" is used between two statements which have 

some kind of relation and also in logic gate "AND"

Disjunction:

~ The disjunction of two statements P and Q is the statement   which is read as "P OR Q".

~ The statement P V Q has the truth value F only when both P and Q have the truth value F; Otherwise 

it is true. 

Example:

P: Today is friday.

Q: It is raining today.

SOLUTION: Today is Friday or it is raining today.

This proposition is true on any day that is a Friday or a rainy day (including rainy Fridays) 

and is false on any day other than Friday when it also does not rain.

Exclusive OR:

~ Le P and Q be prepositions.

~ The Exclusive OR of P and Q is denoted by  or which means "either  or  but not both".

~ The proposition that is true when exactly one of P and Q is true and is false otherwise. 

~ The exclusive or  is True when either p or q is True, and False when both are true or both are 

false.

~ The truth table for the Exclusive OR of two propositions.

Example:

P: Today is friday.

Q: It is raining today.

SOLUTION:    is “Either today is Friday or it is raining today, but not both”. This 

proposition is true on any day that is a Friday or a rainy day (not including rainy Fridays) and 

is false on any day other than Friday when it does not rain or rainy Fridays.

Conditional or Implication:

~ Let P and Q be prepositions. The implication  or " P then Q" is the proposition that is 

false when P is true and Q is false and true otherwise.

~ In this implication P is called the hypothesis or antecedent or premise.

~ Q is called the conclusion or consequence.

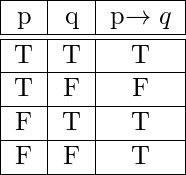
~ This follows from the Explosion Principle which says - “A False statement implies anything” Conditional statements play a very important role in mathematical reasoning, thus a variety of terminology is used to express , some of which are listed below.

"if , then "
" is sufficient for "
" when "
"a necessary condition for  is "
" only if "
" unless "
" follows from "

Example:

P: Today is friday.

Q: It is raining today.

SOLUTION:  "If it is Friday then it is raining today” is a proposition which is of the form 

. The above proposition is true if it is not Friday(premise is false) or if it is Friday and 

it is raining, and it is false when it is Friday but it is not raining.

Bi-conditional or Double Implication or Bi-implication:

~ A statement made both from the conditional and converse.

~ The bi-conditional of P and Q, denoted by  or " if and only if(iff) ”.

~  has the same truth value as .

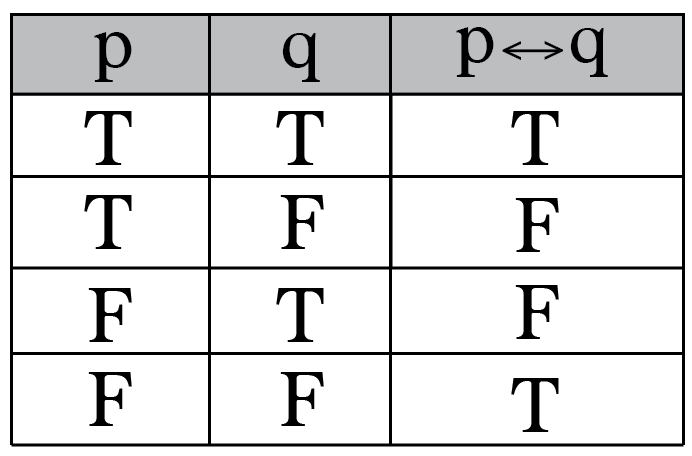
" is necessary and sufficient for "
"if  then , and conversely"
" iff "

Example:

P: Today is friday.

Q: It is raining today.

SOLUTION: 

“It is raining today if and only if it is Friday today.” is a proposition which is of the form 

. The above proposition is true if it is not Friday and it is not raining or if it is Friday 

and it is raining, and it is false when it is not Friday or it is not raining.

Tautology:

A statement formula which is true regardless of the truth values of the statements which replace the 

variables.

Example:

p → p, p ∨ ¬p, and ¬(p ∧ ¬p) 

Contradiction:

A statement formula which is false regardless of the truth values of the statements which replace the 

variables.

Note:

* The negation of a contradiction is a tautology.

* A statement formula which is a tautology is identically true and a formula which is a contradiciton is 

identically false.

Logical Equivalence:

* The most useful class of tautologies are logical equivalences.

* This is a tautology of the form X ↔ Y , where X and Y are compound propositions.

* In this case, X and Y are said to be logically equivalent.